Disjoint Set

TODO

A disjoint set in computer science is a data structure that stores a collection of disjointed (non-overlapping) sets.

Operations

Disjoint sets data structures will generally provide the following operations:

• Adding a new set
• Merging sets
• Finding a representative of a set

Explanation

The idea behind disjoin sets is to represent data that is most easily thought of as non overlapping sets, as mentioned above. One common example is for social connections. Imagine you have 8 people, denoted by the first 8 letters of the alphabet. Let’s say A is friends with B, B is friends with D, C is friends with E. H is friends with F, and G is friends with no one. This can more easily be represented by a collection of sets as such:

$$\begin{array}{rl}{S}_0& =\{A,B,D\}\\ S_1& =\{C,E\}\\ S_2& =\{H,F\}\\ S_3& =\{G\}\end{array}$$

So how do we know if people are friends with each other?

Well, the way disjoint sets do it in computer science is to chose a representative of a set. Then, we check if two people have the same representative, and if they do, they’re in the same set. In our above example, we can say that $A$ represents the set $S_0$. Both $B$ and $D$ agree that $A$ is their rep. You then go ahead and ask them who their rep is, and if they say $A$, they’re part of that set and thus friends with $B$, $D$, and $A$ (and are one of them). If they say any other person, then they don’t belong in that set.

Implementation

So how do we translate the above idea? With an array that contains a pointer to a tree, or some kind of indicator of emptiness or root-ness, usually -1.

More specifically, an element of that array will either have no representative (-1), in which case it is has no parent, or it will point to another element of the set, forming a sort of tree that represents the set.

The invariant of disjoint sets is that every element points to its parent, and following parent pointers always leads to a root that represents the entire set.

So, let’s imagine an array with four values to start off with, $[-1,-1,-1,-1]$. So this represents four different elements in that array that are all separate, since they are all roots.

Here is our initial, naive implementation of the disjoint set structure with its three operations. Let parent be the dynamically sized array mentioned above.

void make_set(int v){
	parent[v] = -1; //create a new entry into the parent array
	//an point it to nothing (-1), root of itself
}
 
int find_set(int v){
	if(parent[v] == -1){
	//if that element of the array is -1, we have found it
	// since it's its own set
		return v;
	}
	return find_set(parent[v]);
	//if it's not, we have to recurse parents until we find it
}
 
void union_sets(int a, int b){
	a = find_set(a);
	b = find_set(b);
	if(a != b || a == -1){
		parent[b] = a;
	}
}

So let’s play around with this implementation a little bit to see how it works. We union two sets, say 0 and 1, the first two spots in our array. A is immediately found, since the value it holds is -1, and same goes for b. Since a == -1, the if condition on line 19 evaluates to true, and we assign b’s spot in the array to the value of a, 0. We therefore end up with the following array: $[-1,0,-1,-1]$. So what does this mean? This means that the second element in our array is now pointing to the first as its parent. Visually, we can reconstruct it as so:

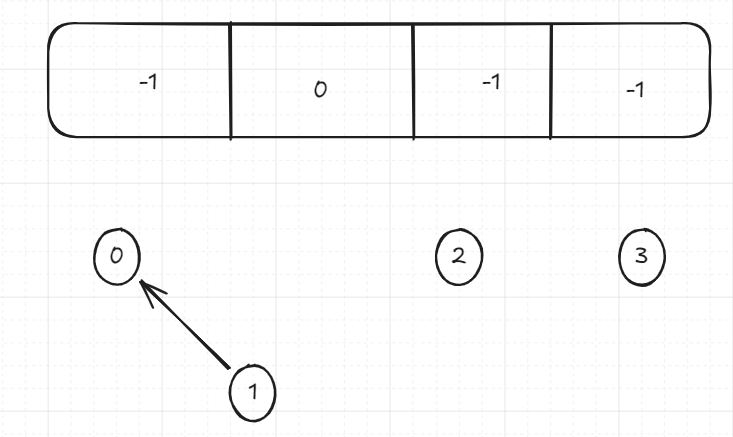
Where we have the parent array up top and our visualization at the bottom. The values in the nodes are their index in the array. So our second node with value 1 is currently pointing to our first node with value 0, which is why in the array it has a value 0. The rest are all at value -1, since they’re pointing to nothing.

Let’s merge another set. Let’s merge the node at index 1 and node at index 2. We find_set(1), which will fail the if statement, since it’s value is 0 and not -1, and will then call find_set(0) recursively. In that call it succeeds, and the whole thing returns 0. Our second find_set call in union_set for b, will immediately return -1. They’re not equal, so we assign 0 toparent[b] / parent[2]. Visually, we end up with the following:

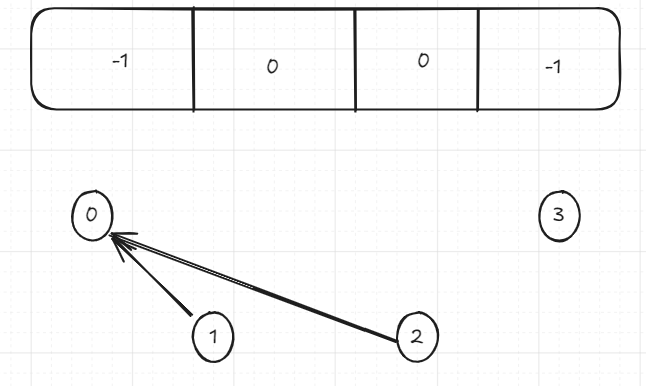
Which is exactly what we wanted, the third element of the array / index 2 is now part of the same set as the second element of the array. They both point to the same representative, the element at index 0.

This implementation works well enough, but it can encounter the adversarial case where you end up with a degenerate tree. In this case, the find_set function ends up having a time complexity of $O(n)$, as many algorithms prone to degenerate trees. Thankfully, there is a way to mitigate this case with the following changes:

int find_set(int v){
	if(parent[v] == -1){
		return v;
	}
		return parent[v] = find_set(parent[v]);
}