A binary tree is a special type of tree that has at most two children per node. They are most useful either when used as a basis for binary search trees or binary heaps, or as a data structure representation for a form of data that naturally bifurcates into two cases, such as Huffman encoding or an ancestry chart.
Implementation
template <typename T>
class Tree {
struct Node {
T data;
Node* left;
Node* right;
};
}An example implementation for an arbitrary data type T.
Traversing Trees
Trees can be traversed in a variety of arbitrary ways but are most commonly traversed in the following distinct three methods. Other alternatives include breadth first search and level order.
inOrder
void inOrder(Node* nd){
if (nd != nullptr){
inOrder(nd->leftchild);
visit(nd);
inOrder(nd->rightchild);
}
}If the tree ingested is a binary search tree, this would visit nodes in growing order. This algorithm recurses until the left base case is reached, then collapses to the right, then upwards.
preOrder
void preOrder(Node* nd){
if (nd != nullptr){
visit(nd);
inOrder(nd->leftchild);
inOrder(nd->rightchild);
}
}Pre order will instead visit every node on its path sequentially, so the first node will always be the root of the tree, and the last will always be the right most node.
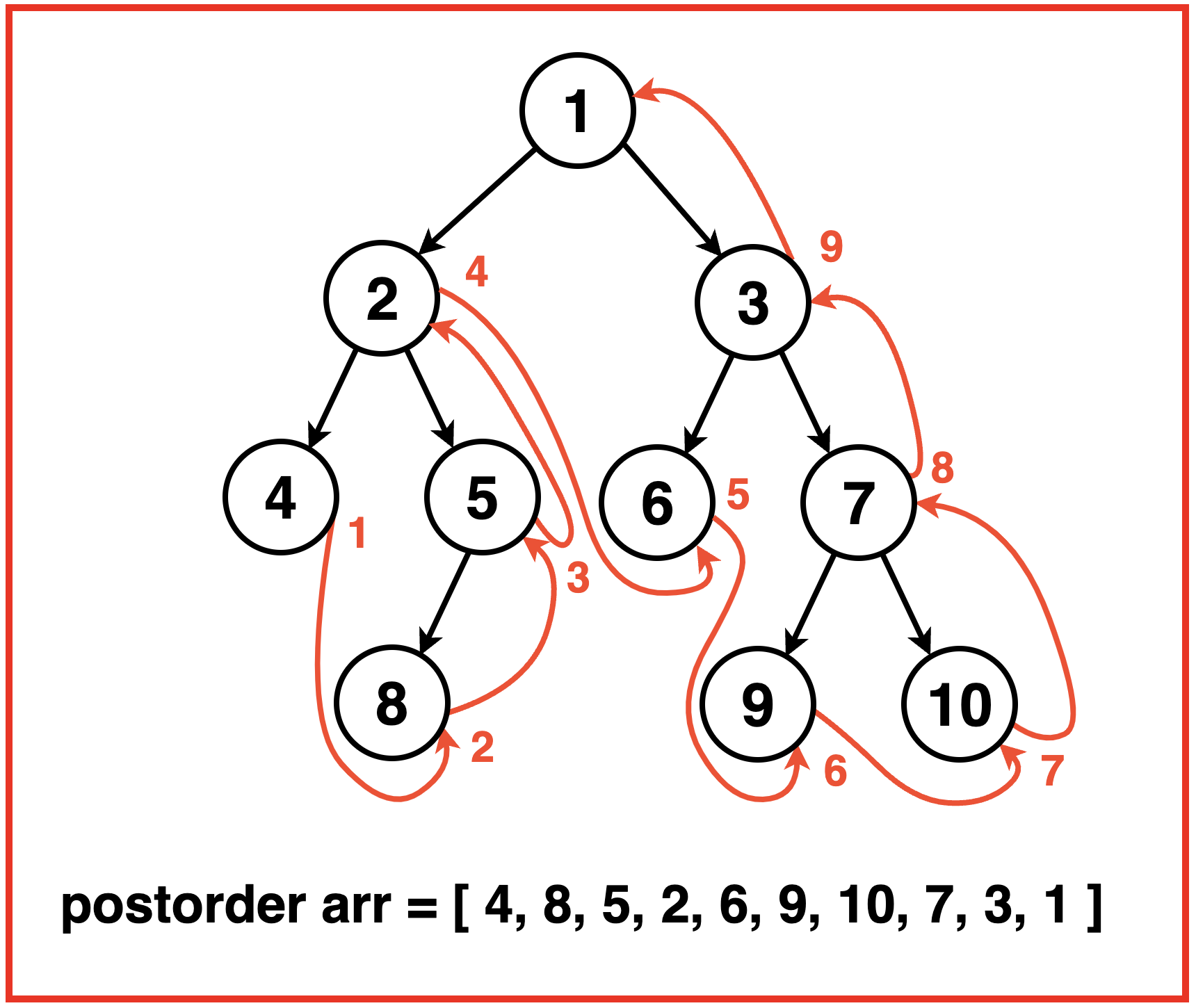
postOrder
void postOrder(Node* nd){
if (nd != nullptr){
inOrder(nd->leftchild);
inOrder(nd->rightchild);
visit(nd);
}
}Similarly to preOrder, this algorithm recurses left until it hits the base case, but will unwind right first before unwinding upwards.
Complexity
The complexity of the above algorithms is all
Since we visit each node once.
In general, since binary trees are subject to the adversary case of the degenerate binary tree, pretty much all operations have worst case .
Types of Binary Trees
Full
A full binary tree is a tree where every node has either 0 or 2 children.
Complete
A complete binary tree is a tree where every level is full except for the last, which is packed left. Complete binary trees have a height of where n is the number of nodes. The last level of the complete binary tree will always have between 1 and nodes. Complete trees are used for the implementation of priority queues and can easily be represented by an array.
Perfect
A perfect binary tree is a tree where all nodes have two children, except for the leaf nodes which are all at the same level. It’s effectively a pyramid. All perfect trees are complete, but not all complete trees are perfect.
Balanced
Balanced binary trees are trees where the left and right subtree’s height differs at most by one. This accounts for all nodes, not just the root node of the tree. Balanced trees are used in the implementation of AVL trees.
Properties
Size
A binary tree of height h has at most:
nodes. If it does have the maximum amount, the tree is a perfect tree.
A binary tree of height h has at least:
nodes, which is of course the case of the degenerate binary tree.
A complete tree has a height of where n is the number of nodes.