Graph Density

Graph density denotes the proportion of edges in a graph that are connected vs unconnected. A simple graph with near the maximum amount of possible edges will have high density, while a simple graph with almost no edges will have low density.

Definition

Let E be the number of edges in a graph, V the number of vertices. Density is defined by the following formula for simple undirected graphs:

$$D=\frac{|E|}{|V|(|V|-1)}$$

And half that for directed graphs.

Properties

Asymptotically, a sparse graph has $O(|V|)$ edges, while a dense graph has $\theta (|V^2|)$ edges.

The maximum possible density is 1, and the minimum density is zero. The definitions for what delimits a sparse graph vs a dense one doesn’t have a clear non-asymptotic delimitation, but as density approaches zero it becomes more and more sparse, while the more it approaches one it becomes more and more dense.

Applications

Graph density can help with determining the breaking point in space efficiency for different data structures, for example at what density does an adjacency list become more efficient than an adjacency matrix.

Example

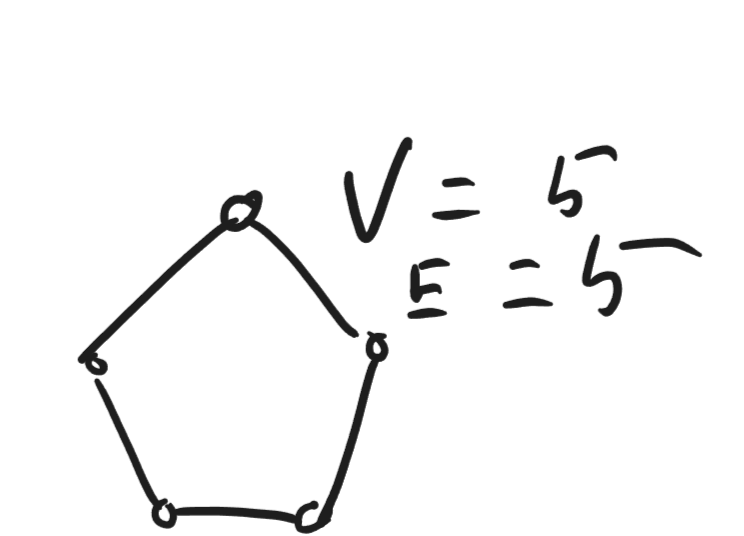
Since the graph above has $V=E$, therefore $E=O(V)$, and the graph is considered sparse.

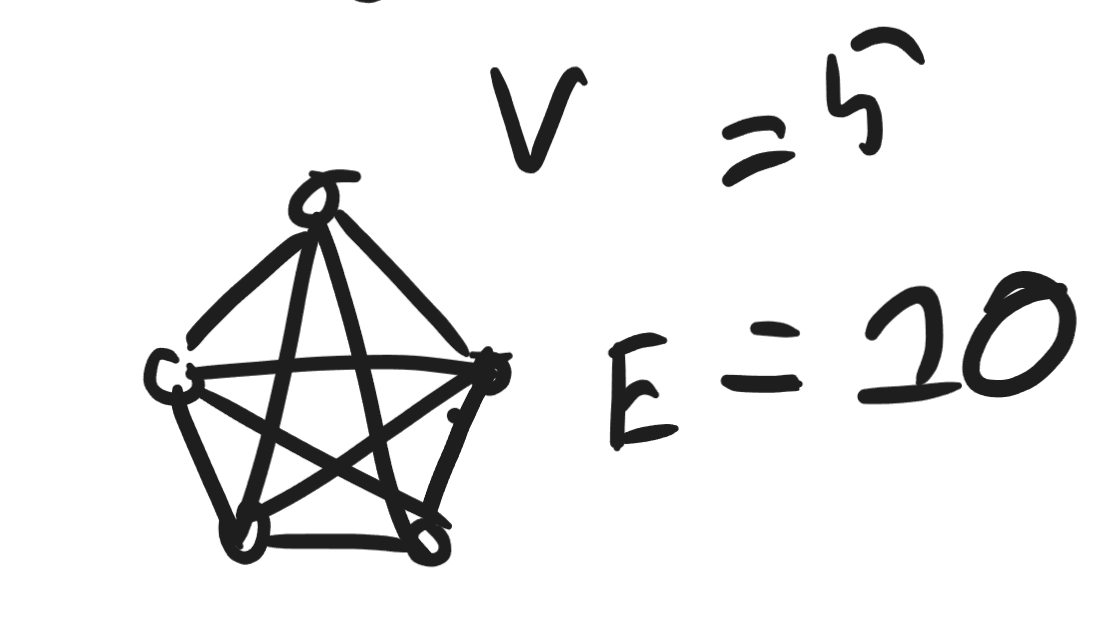
Since the graph above has $E>V$, therefore $E\in \theta (V^2)$ and $E\notin O(n)$ therefore the graph is considered dense.