An adjacency list is a collection of unordered lists used to represent a finite graph. Each unordered list within an adjacency list describes the set of neighbors of a particular vertex in the graph. This is one of several commonly used representations of graphs for use in computer programs.
Representation
Adjacency lists are most easily conceptualized as a table that associates a certain vertex with the collection of its neighboring vertices or connected edges. For example, consider the following undirected graph:
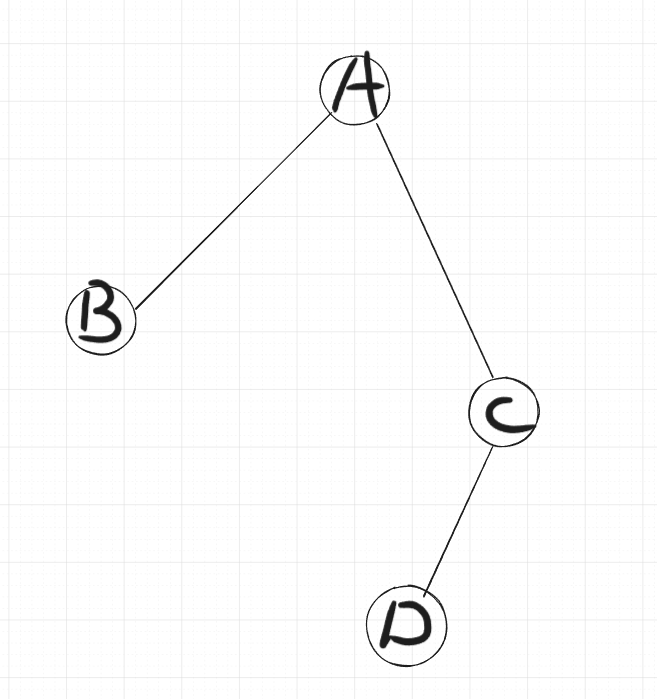
It can be represented with the following adjacency list based off of vertices or edges:
| vertex | adjacent to | vertex list | edge list |
|---|---|---|---|
| A | B, C | AB, AC | |
| B | A | AB | |
| C | A, D | AC, CD | |
| D | C | CD |
Note
The edges should also just have a separate name, I was just a bit lazy : )
Implementation
An adjacency list effectively has to be some kind of list of lists. A few common implementations are a hash table with each element of the table being an array or a singly linked list of the adjacent vertices.
Operations
The main operations for an adjacency list are reporting the list of neighboring vertices or edges of a given vertex. This can be performed in constant time per neighbor. In other words, the cost of finding all neighbors of a vertex is proportional to the degree of V.
Alternatives
The main other alternatives to graph representations are the adjacency matrix.
Tradeoffs
Because an adjacency matrix represents whether an edge is present with a single bit, it is very space efficient on dense graphs, occupying bits of contiguous space. However, because an adjacency list only represents the neighboring vertices/edges that do exist, an adjacency matrix will be more space efficient if the graph is sparse enough. The exact graph density at which an adjacency list becomes more space efficient is .