Depth First Search

Depth first search, or DFS is a core algorithm used to traverse trees and graphs. Much like BFS, it starts at an arbitrary node and explores the graph until it finds a spanning tree. The main difference is that instead of using a working queue to store nodes to visit, depth first search will instead usually use a stack.

Implementation

An example implementation of depth first search could look something like the following:

typdef enum {VISITED, NEW} state;
 
void DFS(Graph G, Node* n){
	Stack s;
	s.push(n);
	n->state = state.VISITED;
	
	while(!s.isEmpty()){
		Node* currentNode = s.pop();
		
		if(currentNode->state != state.VISITED){
			currentNode->state = state.VISITED;
			
			for(Node* adjNode : G.getAdjacentNodes(currentNode)){
				s.push(adjNode);
			}
			
		}
	}
}

It is quite simple in its implementation. There is also a recursive implementation that is quite similar.

Tip

Much like a lot of other algorithms in CPSC 221, you’re not expected to implement them by heart off the top of your head. However, you are expected to know how they work and trace through an example.

Example

Try tracing the following graph implemented with an adjacency list with DFS starting at node A.

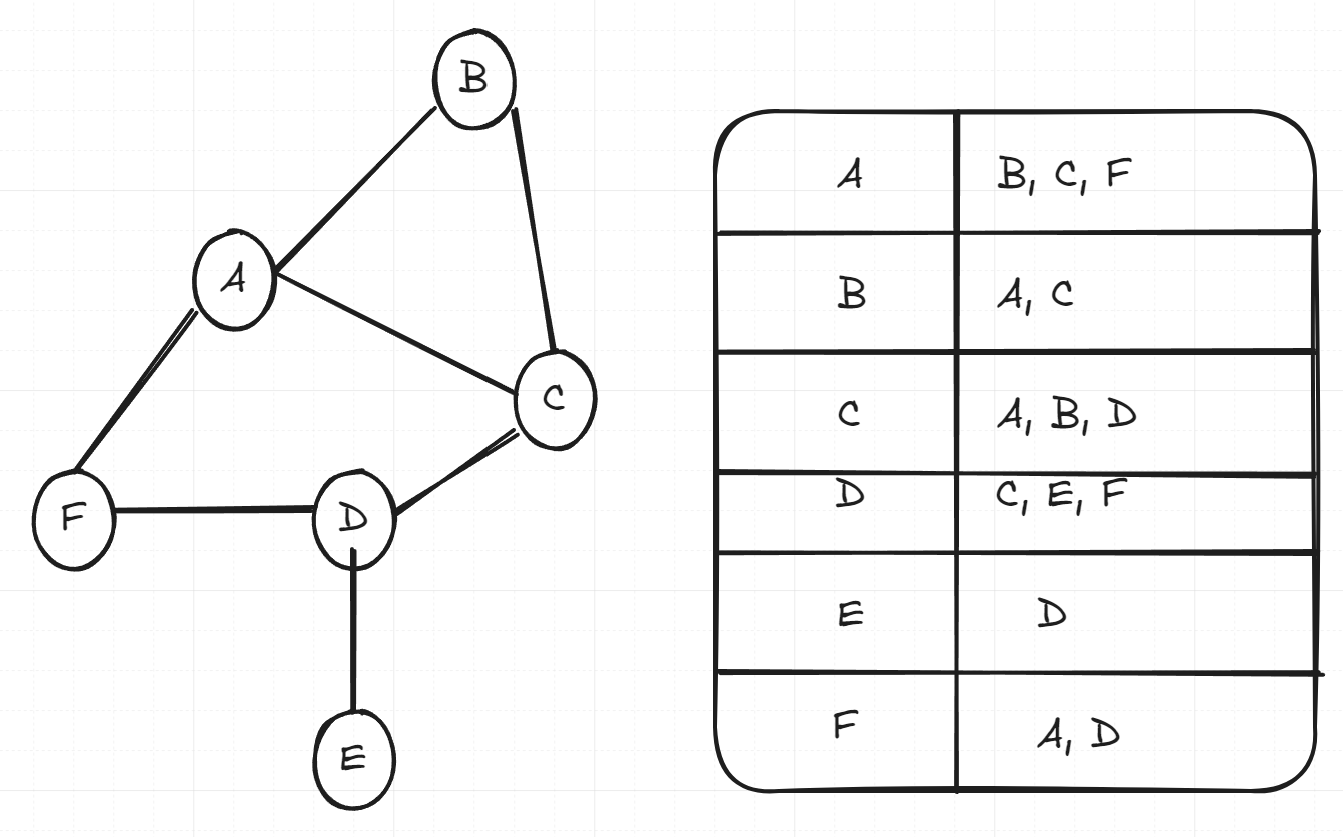
Answer

Visiting A first, we push B, C, F on the stack. We then pop B, mark it as visited, and push A and C on the stack. Our stack now contains from top to bottom, A, C, B, C and F. Since we’ve already visited A, we pop and skip it. We pop C, which is is unvisited so we push A, B and D on the stack. A and B have both been visited, so we visit D. We push C, E and F on the stack. C has already been visited, so we visit E. E only has D, which we push and ignore. F is next, we visit F and push A and D onto the stack. All the nodes have been explored, so we iterate and skip the rest of them and complete our traversal. The final order of our traversal was A, B, C, D, E, F.

Time Complexity

The time complexity of using depth-first search using an adjacency matrix is

$$O(n^2)$$

But when maximally efficient using an adjacency list, the time complexity is:

$$O(|V|+|E|)$$

Where V and E are the number of vertices and edges respectively.