Graph

A graph is a collection of vertices or nodes, connected by edges. A tree is technically a special type of graph.

Definition

Let $G$ is a graph, $V$ are the vertices of that graph and $E$ are the edges of that graph.

Formally, a graph is a set of pairs of edges and vertices such as:

$$G=(V,E)$$

$V$ is a set of vertices (representing potentially anything):

$$\{v_1,v_2,\dots ,v_n\}$$

$E$ is a set of edges:

$$\{e_1,e_2,\dots e_n\}$$

where each $e_i$ is a pair of vertices:

$$e=(v_1,v_2)$$

Terminology

Important

I’ve found that understanding what each type of graph means and represents is super important for CPSC 221, it’ll make it a lot easier to answer more complicated theoretical questions about graphs. Thankfully, for the most part the names are pretty self-descriptive.

Directed

If each edge is an ordered pair that is not commutative, i.e

$$(A,B)\ne (B,A)$$

then the graph is directed, otherwise the graph is undirected. Directed graphs are sometimes alternatively called digraphs.

Simple

A graph is simple if it does not allow for self-loops and multiple edges to the same vertices.

Subgraph

A subgraph is a portion of the original graph. Importantly, you cannot have hanging edges where an edge doesn’t connect to anything.

Degree

The degree of a vertex in a graph is the number of other vertices that it connects to. Degrees are only relative to a vertex, the degree of a graph is semantically meaningless.

Path

A sequence of vertices connected by edges. A simple path is a special type of path with no repeated vertices.

Cycle

A cycle in a graph is a path with the same start and end vertex.

Weighted graphs

A weighted graph is a graph where the edges are weighted in some way or another, for example in CSPC 110 we effectively had the travelling salesman problem with the edges of a graph having distances being the cost in between nodes on a graph. In general, graphs will be weighted with a numerical value representing some kind of cost.

Complete graph

A complete graph is a graph where all vertices are connected with each other. This can for example be represented by a pentagram. In this case, the amount of edges, and in general the maximum amount of edges for a certain graph is (where n is the amount of vertices):

$$n(n-1)$$

If the graph is directed, half that if it is undirected.

Connected

An undirected graph is connected if there is a path between any two vertices.

Properties

A connected graph has at minimum $n-1$ edges.

Strongly connected

Directed graphs are strongly connected if there is a directed path from any vertex to any other.

Applications

Graphs are generally used for storing and computing things that are “networks” by nature. Things like road networks, airline flights, connections etc. Compilers are also an example. Where call graphs are which functions call which others. Graphic meshes are also another example of a graph.

Non-testable

Exam scheduling in an academic setting is an example of an np-complete problem that is solvable with graphs, or the famous travelling salesman.

Handshaking theorem

The handshaking lemma is the statement that in every finite undirected graph, the number of vertices that touch an odd number of edges is even. This is because the sum of the degrees equals twice the number of edges. Since this is the case, the number of vertices that have an odd degree must be even, since the product of an even an odd number is even.

Graph density

A sparse graph has $O(|V|)$ edges, while a dense graph has $\theta (|V^2|)$ edges.

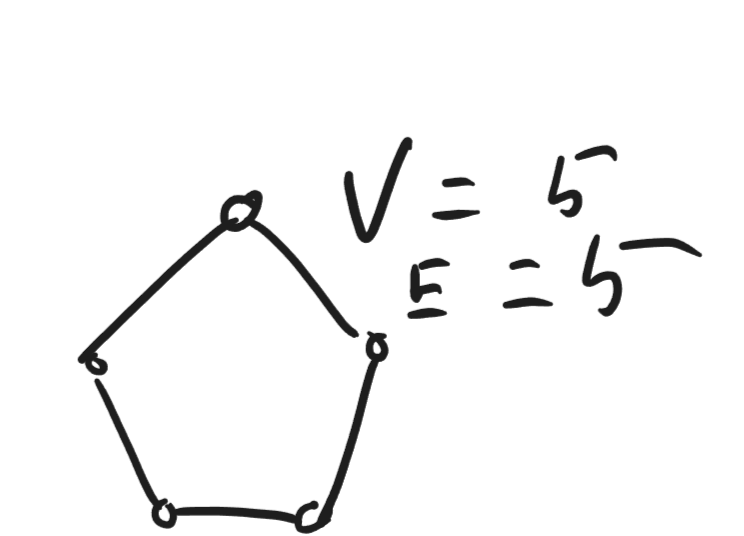
For example the above is a sparse graph.

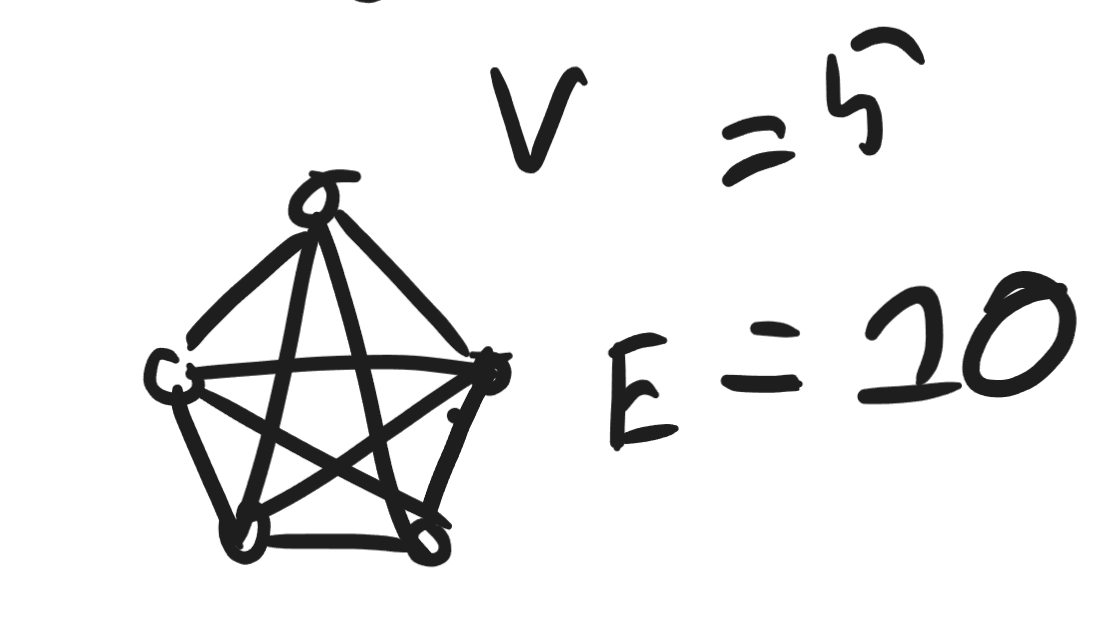
While this would be considered a dense graph, it seems exactly what defines as sparse and dense is not always agreed upon, though asymptotically it is generally defined as above.

For more, see graph density.

Properties

The sum of all degrees in a graph is equal to twice the number of edges. Formally, where $m$ is the amount of edges:

$$\sum deg=2m$$